问题描述:
给出一张图,节点有n个,总共有k种颜色,将k种颜色分配给这n个点,使得在图中的每条边所连接的两个点的颜色不同。这是一个NP问题,如果从精确算法去求解,则会很难在多项式时间内确定求解,所以我们从组合优化的角度对其进行求解。下面描述了禁忌搜索算法和多种混合进化算法处理思路。
启发式搜索
1.禁忌搜索
第一步:随机产生一个初始解,即将每个点随机分配一种颜色,并计算f, f代表当前解的矛盾数(矛盾是指相邻节点颜色相同)。可以利用所有的矛盾数相加除以2求得。
第二步:初始化M矩阵,M是一个二维矩阵(如下图),记录每个点着不同的颜色的不同矛盾数。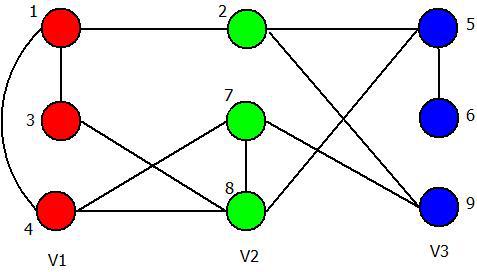
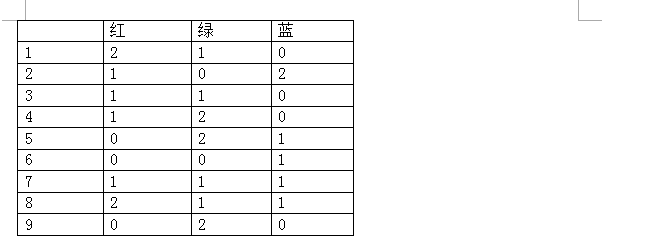
第三步:判断是否有解即每个点涂色后对应的M都是0。可以用f=0表示有解, 若有解则退出。
第四步:若不解,则需考虑能使f最快下降的Δf, Δf理应是个负数, 但是陷入局部最优的时候也是可以接受正数的, 考虑非禁忌的最好解, 保存最小的Δf, 若有多组最好解则按照1/n的概率选择新的最好解。禁忌的最好解的处理方式也是同样的。
第五步:若禁忌的最好解严格优于非禁忌的最好解且严格优于历史最优f_best,则接受禁忌的最好解,否则接受非禁忌的最好解。
第六步:更新M表,并且将新加入的解设为禁忌解,禁忌长度为当前迭代次数+当前矛盾数+1到10的随机数。再走第三步。(如何区分禁忌解与非禁忌解,如果禁忌长度大于当前迭代次数则是禁忌解, 否则解禁为非禁忌解。)
2.混合进化搜索
混合方式: 交替选择父代中图同颜色最多的组,依次标上1~k种颜色, 然后去掉属于该组的所有元素, 最后若有未被分配的节点, 则随机涂色。如图所示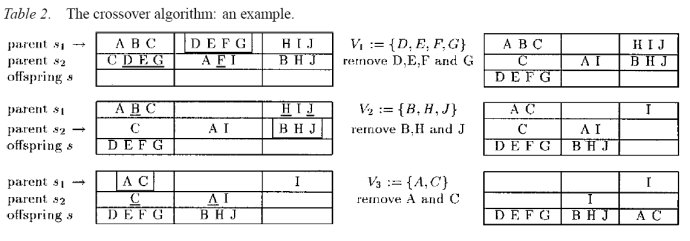
混合进化1:
十个子代构成种群,随机选择两个进行杂交(杂交方式如上图),然后将结果进行禁忌搜索,用得到的新解,替换原先的十个种群中最差的解,(ps:一种是直接替换最差的解,一种是新解比原先最差的解要好的时候才替换。其实测试两种效果差不多。)
混合进化2:
只有两个初始解,将两个解作为父代s1,s2.s1杂交s2得到一种解s1’,s2杂交s1得到一种解s2’,将s1’禁忌得到的解直接替换替换s1,将s2’禁忌得到的解直接替换替换s2,重复操作。直至求解。
混合进化3:
思想和第二种大致相同,但是它会在每次把上一个十代的最好解替换当前的某个父代。这种方法是考虑到疏散性与集中性的平衡,其实生活的哲学也是一种平衡。这种处理方法是最快能够求解的,如果需要源码和测试案例可以邮箱联系我。
结论
对于NP问题的研究感觉需要很多灵感,需要借鉴各个领域的知识,这也从另一方面说明了计算机科学是一个舶来品的科学。关于NP?=P一直都无法解决,很多研究人员所做的事情更像是炼丹,炼出来的结果不错就可以发论文。当然解决这些问题本身也是很有趣的,也很有价值,如果将每个点都赋予权值,就会有sum-coloring问题,如果再把每个点当成集群的节点,就会有比如负载均衡,资源分配的问题。